Options trader Alan Ellman of TheBlueCollarInvestor.com explains how your knowledge of skew and smile patterns can help you better understand the relationship between implied volatility and option premiums, thus better help you assess potential risk in the future.
In covered call writing, our option premiums are influenced by the volatility of the underlying security. Using the Black Scholes option pricing model, we can calculate the volatility of the underlying by entering the market prices for the options. Common sense would seem to dictate that for options with the same expiration date, we expect the implied volatility (IV) to be the same regardless of which strike price we use. However, in reality, the IV we see is different across the various strikes. This disparity is known as the volatility skew. Let’s first review some key definitions:
Implied Volatility - This is a forecast of the underlying stock’s volatility as implied by the option’s price in the marketplace. This differs from historical volatility:
Historical volatility: This is the actual price fluctuation as observed over a period of time.
As discussed in my books and DVDs, an options pricing model such as the Black-Scholes model uses six inputs to determine the theoretical price of an option:
- Asset Value
- Time Left Until Expiration
- Strike Price
- Risk-Free Interest Rate
- Dividends (if applicable)
- *Asset Volatility
Option premiums will rise and fall with volatility. These pricing models make the incorrect assumption that volatility is constant throughout each respective strike price and regardless of duration. Supply and demand will never allow these conditions to exist. It is, however, possible to calculate IV for different strike prices and over different time frames by using the current options price as a given, using the other five inputs listed above and then solving for that specific IV. The difference in implied volatility levels for options with the same underlying security is known as volatility skew. Stated differently, it is the difference in IV between out-of-the-money, at-the-money and in-the-money options and also different expiration periods.
NEXT PAGE: Different Types of Skews
|pagebreak|Types of Skews
1. Vertical Skews (different strike prices):
The two types of vertical skews are forward and reverse. The reverse skew, which is common to the equity market, is where the lower option strikes have higher IVs and the higher strikes have lower IVs. The downside options are being priced more aggressively to put more premium on fast downward moves, which intuitively makes sense. If we plotted the IVs over the various strike prices, here is what a typical skew chart would look like:
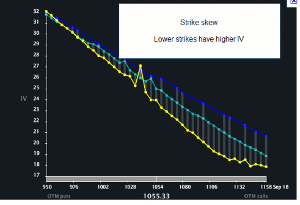
Skew chart for strike prices and IV
Click
to Enlarge
2. Horizontal Skews (same strike, different expirations):
Horizontal skew refers to the situation where at a given strike price, IV will either increase or decrease as the expiration month moves forward into the future. A forward horizontal skew occurs when volatilities increase from near to far months. This is typical of the equity market. A reverse horizontal skew occurs when volatilities decrease from near to far months. Below is a chart showing a forward horizontal skew for the S&P 500:
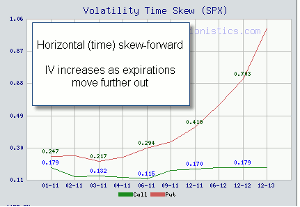
Forward horizontal skew
Click
to Enlarge
3. Skew Smirks and Smiles
Although volatility skew (see the top chart) is most typical for equity strike price, we occasionally see volatility smile or smirk. This could occur when there is anticipation of extreme market or stock price movement, like an earnings report or other corporate news. This can result in speculators buying the out-of-the-money options to take advantage of the potential price movement. As a result the IV of the higher strikes will rise thereby changing the skew to a smile or smirk pattern as shown in the images below:
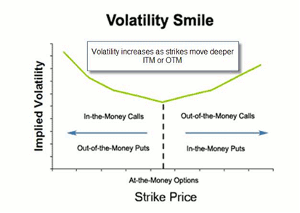
Classic Volatility Smile Pattern
Click
to Enlarge
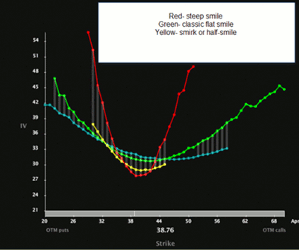
Volatility smiles and smirks
Click
to Enlarge
In these instances the I-T-M and O-T-M strikes have higher IVs (more expensive) than the A-T-M strikes.
Sites to build skew charts
Free: http://www.optionistics.com/f/volatility_skew
Not free but sophisticated: www.livevol.com
Conclusions
By studying the IV chart patterns we know that the volatility assumptions made by option pricing models rarely exist in the real world. IVs ARE different across different strikes and time frames. Generally the market assigns a higher IV for lower strikes and higher IVs for longer durations for the same strikes. These typical stock IV patterns result in skew patterns. When a skew develops into a smile, there is an expectation of greater price movement in the future, causing the chart pattern to turn up into a smirk or smile.
By Alan Ellman of TheBlueCollarInvestor.com





















