As part of our continued efforts to explain the major technical indicators to MoneyShow.com readers, what follows is a simple explanation of the Stochastics momentum indicators often used in our analysis.
Originally devised by George C. Lane in the 1950s, the Stochastic oscillator is one of the easiest indicators to interpret. It tells us where the price sits in relation to its recent trading range, in a fixed 0 – 100 range, and using different degrees of smoothing to provide some stability. Coming in a few different versions, their interpretation rests on the sensible assumption that price pressure is on the upper end of the range in an uptrend, and on the lower end in a downtrend.
Before we create a Stochastic oscillator, we need to decide what time parameter to use. Ten periods is our preferred choice for our daily charts, capturing the range of the previous two weeks.
The simplest one, the fast Stochastic, has two lines: %K and %D, calculated as follows:
• %K = [close – low (N-range)]/[high(N-range) – low(N-range)]
• %D = SMA (%K)
So %K is the position of the most recent close in the range of the last N days; if the close was the low, we get 0; while if the close was the high, we get 100. And %D is the simple moving average of this series (we also need to choose a period for this moving average; typically, we use 3).
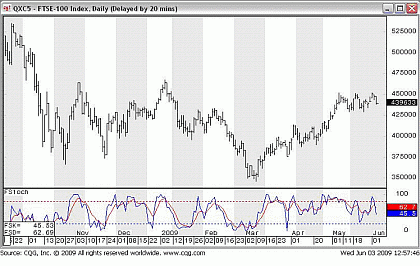
Fig 1. Fast Stochastics
It’s always helpful for an indicator to be bounded in a constant range, such as this is between 0 and 100. For one thing, we don’t need to worry about long-run matters like inflation. You’d get a similar pattern for an uptrend in the Dow whether you were looking at it in 1950 or 2000, without any need to rescale it. This means we can easily look for recurring patterns in a market over a period of decades.
It also means that we can easily use the indicator for intermarket analysis. Since the oscillator is bounded as it is, the patterns have the same size regardless of whether you’re watching a stock that trades for £1.00, £20.00 or £50.00, a currency pair, or an interest rate future.
Getting back to the main topic, the only major problem with the fast Stochastic is the lack of smoothing. Note how jagged the %K (blue) line is in the FTSE Index chart above. It reaches extreme readings quite frequently, jumping about and making it hard to interpret.
The solution is easy: We use the smoother red line of the fast Stochastic as our blue %K line instead, and then average it and use the new average as our new red line. So the new red line is the average of the average of the old blue line (simple, isn’t it?), and this is how we construct the “slow Stochastic.”
Fast Stochastic:
- %K = position in N-range
- %D = SMA (%K)
Slow Stochastic:
- %K = %D (fast Stochastic)
- %D = SMA (%D (fast Stochastic))
NEXT: Comparing Fast and Slow Stochastics
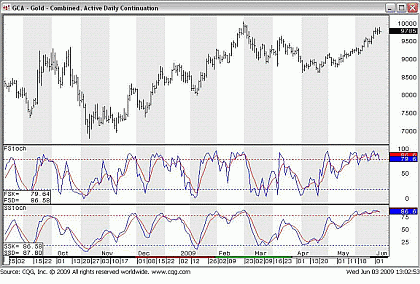
|pagebreak|Fig 2. Fast Stochastics vs. Slow Stochastics
We can compare the different Stochastics in the chart above. Observe that the slower red line in the fast Stochastic is identical to the faster blue line in the slow Stochastic.
Now we can see the advantage of the slow Stochastics. They don’t reach the overbought/oversold levels so easily, meaning that we are whipsawed less frequently.
What are these overbought and oversold levels? Generally, we consider anything above 80 to be overbought, and anything below 20 to be oversold.
This system of lines provides a bunch of easily observed buy/sell signals. The simplest of these is simply to take a buy signal when % K crosses the slower % D line from below and a sell signal when it crosses from above. However, this generally happens much too frequently to provide useful signals.
The solution most commonly used is to wait until the slower %D line makes it into one of the extreme overbought/oversold regions, and only use crossovers that occur there. This gives us fewer false signals, and with those we do get more likely to be at genuine market turning points.
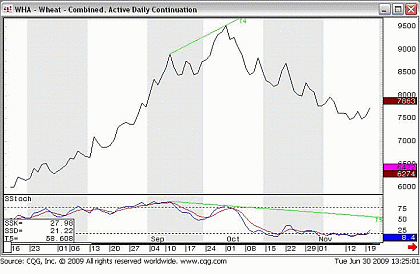
Another technique that Stochastics have in common with other indicators is divergence—when the oscillator moves in the opposite direction to price. This is a warning sign that a trend is running out of momentum. So, for example, if we have an uptrend on the price chart with a sequence of higher highs being formed, but the Stochastics are forming a sequence of lower lows, then we can say that the uptrend is losing momentum, and that we will give extra weight to any argument that a reversal is underway. The chart below illustrates one of those divergence scenarios with a resultant selloff.
Fig 3. Divergence of Price and Slow Stochastics
As with other oscillators, the biggest danger when using it is to assume that a reversal is imminent simply because it is at an extreme measurement. This isn’t necessarily true! Price pressure will remain on the upper end of the range, and hence, the Stochastic will stay at elevated levels for as long as the market is trending.
NEXT: More Case Studies on Using Stochastics to Find Good Trades
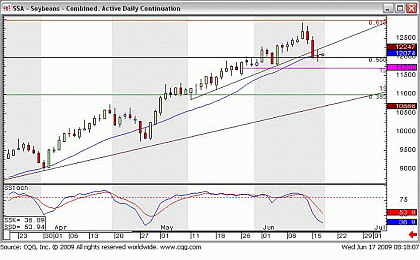
|pagebreak|Fig 4. Sustained “Overbought” Stochastics Measurement
In the soybeans futures market recently, for example, the slow Stochastics remained in the overbought region from May 6 to June 11. Why wait for a reversal through all of time, instead of just running with the trend? The Stochastic crossover signal is an excellent countertrend signal, but that’s not much use when the market just keeps on trending.
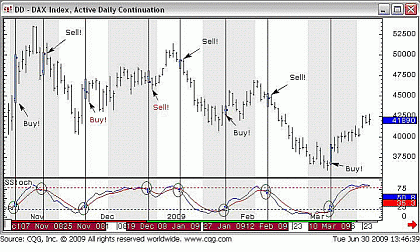
This would have been a better market to trade with the Stochastics:
Fig 5. Ranging Market with Useful Stochastic Signals
We weren’t so strict as to wait for the %D (red) line to get into overbought/oversold territory before we accepted a signal, but most of them worked pretty well. The two signals in red font weren’t successful (we were mostly flat after the red buy signal, and the market rallied after the red sell signal), but six of the eight crossovers were followed by decent moves in the direction of the signal.
The lesson: Always adapt your indicators to the market you’re trading, and remember that even when it appears to be working, no signal is infallible!
By Graham Neary MSTA
Contact Graham at either graham@futurestechs.co.uk or at Futurestechs.co.uk