This article is a sequel to last week’s article explaining the basic concept of LEAPS (long-term equity anticipation securities). It focuses on two specifics that were not discussed in part one: namely, implied volatility and directional moves.
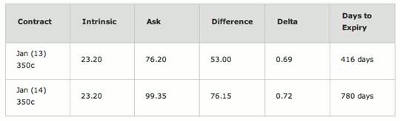
The previous article displayed the figure below, showing the specifics of two Apple (AAPL) LEAPS that are expiring a year apart. The values listed in Figure 1 are the contract’s strike prices, intrinsic value, asking price for the premium, Delta, and days to expiry.
After emphasizing the importance of the intrinsic and Delta values in the last article, let us now move onto the column labeled “Difference.” It actually means extrinsic value and is often referred to as the time value.
For instance, the January 2013 call contract with a strike price of $350 has an intrinsic value of $23.20 (AAPL sitting at $373.20 = $350 + $23.20). Yet the premium of that contract is overpriced by $53.00 because its asking price is $76.20.
Is all of that $53.00 truly caused by having 416 days to expiry, or is there something else?
Click to Enlarge
Figure 1: AAPL @ 373.20 on the close of 11/28/2011
Yes, there is something else. There is an additional component of the extrinsic value that is often invisible, and also highly understood. This piece is the IV (implied volatility).
See related: 3 Things All Option Traders Must Know
The IV reading could be high, low, or in the middle range. Yet, let us state for the record where AAPL’s implied volatility was on 11/28/2011 in relationship to its 52-week high and low.
Click to Enlarge
Figure 2: AAPL IV on 11/28/2011
The current IV of 34.54% in relationship to its 52-week historical volatility high was only 5.64% away from its high, while it was 24.27% away from its historical low. This means that the option premiums were overpriced.
Having said that, we could conclude that there was definitely a better time to buy the AAPL LEAPS than right at that moment.
NEXT: Component 2: Directional Moves
|pagebreak|Let us move our focus onto the directional move. A day after the first article’s figures were taken, the Dow Jones Industrial Average rallied nearly 500 points. Consequently, AAPL also made a significant move—nine points, to be exact.
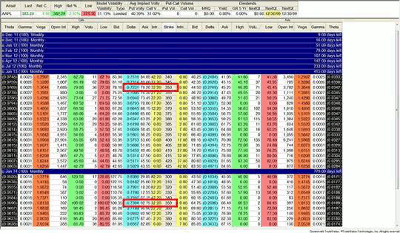
Figure 3 is the snap shot of the option chain after the close of 11/29/2011.
Click to Enlarge
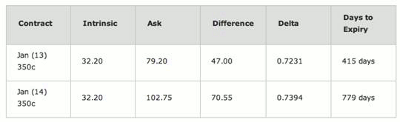
Figure 4 below is actually a table which shows the change that has taken place in the two LEAPS. Observe carefully what took place only a day later in terms of the overall premiums of these LEAPS versus what those values were in Figure 1.
Click to Enlarge
Figure 4: AAPL @ 382.20 on the close of 11/29/2011
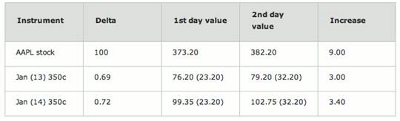
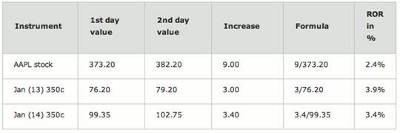
Just in case the point is not clearly observable to everyone, there is another way of looking at this. Let’s simply compare the stock with the LEAPS and look at these selected facts: Premium value and Delta.
Click to Enlarge
Figure 5: Intrinsic Value is in parentheses
At this point, anyone looking at the table above can observe that the stock had moved up nine points while the premium gained only about one third of that move.
Is that normal? Is the math behind this correct? How could this be possible; isn’t the Delta stating that for every hundred cents of the underlying asset’s move up, our option premium should increase in the amount of the Delta?
If that is correct, then our 70-cent Delta times nine points of the AAPL move up should give us (.70 x 9) 6.30, which must be added to the premium. The value of the premium should increase by 6.30, right?
Yes, if the assumption is made that overall premium is composed of just intrinsic value. However, that is not true because the overall premium has extrinsic value, which itself has both volatility and time decay built in. (An option trader cannot be biased, just adding the increase of the Delta and ignoring what is taking place with the other Greeks.)
See related: Know Your Option “Greeks”
Let us ask ourselves the following question: What tends to happen to the implied volatility when the market rallies? It goes down; therefore, the amount of volatility needs to be subtracted from the extrinsic value.
Also, an additional component that must get subtracted is the Theta, or time decay. To recap, the Delta has increased, but Vega and Theta have dampened the increase of the Delta. However, even with this dampening, the option investment in the LEAPS has made a better rate of return (ROR) as compared to just owning the stock.
Click to Enlarge
It is fitting to summarize this scrutiny of the LEAPS performance versus the outright stock ownership by asking: What if the scenario was not so good and the underlying had gone in the opposite direction of what we had initially planned? Would we be complaining about it then? Would we then be asking why we lost only one third?
By Josip Causic, instructor, Online Trading Academy
