Today, options expert Russ Allen, of Online Trading Academy, outlines the options method that involves selling stocks and replacing them with a combination of interest-bearing deposits and call options.
Let’s say we have a portfolio of stocks worth one million dollars and we are concerned that the market could drop substantially from here. Despite our concern, we also know that the market could continue to rise and so we are reluctant to sell out and then be left behind completely.
I’ve left this method for last, because the current environment is not the most favorable one for it. I’ll explain why below.
In its simplest form, here’s what it would involve:
- Sell the stocks.
- Calculate the amount of money that could be earned in the next year on a risk-free interest-bearing account, on the cash generated from the stock sale.
- Deposit the amount of cash in that interest-bearing account that will grow back to the full portfolio value in a year, at the risk-free rate now available.
- Use the balance of the cash to buy call options.
- In a year, the interest-bearing account alone will once again be equal to the full current value of the portfolio.
- If stocks have gone down, the call options will be worthless and the net profit/loss will be zero. There will be no net loss in the portfolio, no matter how low stock prices have dropped.
- If stock prices have gone up in a year, the call options will show a profit, which is unlimited. The value of the call options at that time, if any, will be the net return on the portfolio.
Using our million-dollar portfolio example:
First, we sell the stocks, generating a million dollars in cash. (We’ll also generate a taxable capital gain, if this is in a taxable account. This will be a factor in determining whether we want to use this method).
Next, we determine how much interest income we could earn with zero principal risk in a year. In the US, the rates paid by the US treasury are used as the risk-free rate. Suppose one-year treasury rates were at their historical average of around 4%. [That is currently not the case, of course. 1-year treasuries are now paying about 0.3%. That’s why this is not the best environment for this method]. In that case, with a 4% yield, our principal size needs to be $1,000,000/1.04, or $961,539, to grow into one million dollars in a year. This is another way of saying that at 4%, the present value of one million dollars a year from now is $961,539.
Third, we use the $961,539 present value amount to purchase the treasury securities.
Finally, we use the balance of the cash—$38,461—to buy one-year call options on one or more stocks or exchange-traded funds. Our principal is safe in any case in the treasuries. So, if we choose to do so and we accept the risks, we could afford to be more speculative in our choice of the underlying stocks. Considering just a selected few alternatives ranging from less speculative to more speculative, we might decide, for example, to use the exchange-traded funds for the NASDAQ 100 (QQQ); the Russell 2000 small-cap index (IWM); the oil drillers fund (XOP); the biotech index fund (IBB); and/or individual stocks in any companies we thought had good prospects.
At the end of a year, our $965K worth of treasury securities will be worth $1 million in any case.
NEXT PAGE: Here’s a Hypothetical
|pagebreak|In the worst case, all of our stocks will have gone down and all our call options will be worthless; we will once again be left with a million dollars in our portfolio. Yet, if any of our stocks or ETFs have gone up in price, then our call options will be in-the-money and will have value. Whatever that value is will be the net return on our portfolio.
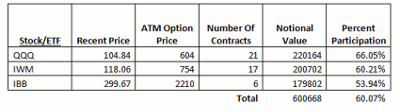
Let’s look at a hypothetical example where we divide up our option portfolio into three equal portions of the options of QQQ (NASDAQ), IWM (Small-Caps), and IBB (Biotechs). We would use 1/3 of our $38,461 option budget, or about $12,800 to buy as many at-the-money (ATM) option contracts on each stock as it would buy. Using options that are as close as we could get to a year away, here are some figures. The column headings in the table are explained below.
In the above table, the Recent Price is the closing price of each ETF as of November 25, 2014.
ATM Option Price is the price per contract of the options with a strike price closest to the Recent Price.
Number of Contracts is the number of option contracts that could be purchased with 1/3 of our option budget, which was $38,461 altogether. This is different than the number of shares we could buy if we used 1/3 of our total $1,000,000 portfolio value to actually buy the stock. How many contracts we can buy depends on how much money we have available to use (higher with a higher risk-free rate of interest income) and on the price of the specific options. These will vary greatly.
Notional Value is the Number of Contracts, times 100 shares per contract, times the Recent Price. This is the amount of stock value that we are controlling with the options that we can afford to buy.
% Participation is roughly the percentage of the increase in the stock’s price that our options will provide to us. This is the Notional Value divided by the $333,333 that we would be able to spend on each stock, if we were using all of our money to buy the stocks.
When it’s all said and done, this particular combination would allow us to participate in about 60% of the profits (if any) on these stocks; and 0% of the losses. A year from now, this would seem a genius move if all of our stocks have gone down, since we will have no net loss. If any of them have gone up, we will have made money. But we will have traded off 40% of our potential profit, in exchange for being completely sheltered against any losses. Whether this is a good deal depends on how much we value the shelter from a bear market.
In summary, here are the pros and cons of this trade:
PRO:
- Bomb-proofs our portfolio, so there can be no net loss of principal.
- Allows us to participate on the upside if markets continue to go up.
- In times of high interest rates, our potential upside is large (although not quite in proportion, since higher interest rates also increase the cost of call options).
CON:
- Generates immediate taxable capital gains from the stock sales, if done in a taxable account.
- Our upside participation is usually less than 100%, because of the limited number of option contracts that can be bought with the available interest earnings.
- In times of low interest rates, the strategy is not really workable, because the amount of available funds with which to buy options is very small.
By Russ Allen, Instructor, Online Trading Academy