Options instructor Russ Allen, of Online Trading Academy, takes a unique approach to this first part of his discussion about the mathematics behind options, by comparing option probability, stock price history, and future movement…to a roll of the dice.
More than most other trading instruments, put and call options represent a game of probabilities. They give us ways to have an edge by evaluating what outcomes are more likely to happen than others and then positioning ourselves to profit if the more likely outcomes do happen. If we make more right trades than wrong ones, and/or win more on each good trade than we lose on each bad one, then we can make money overall.
In beginning this discussion on probabilities, let’s define a couple of terms. If you are not at all interested in the mathematics behind options, please feel free to tune out. But, if that’s true…you are probably not reading this article anyway. For the rest of us, let’s get down to it.
When thinking about what values of something are the most likely at some time in the future (the price of a stock, for example), one way to start is to look at what values we have seen in the past. When we approach it this way we are implicitly making an assumption: that the future will look pretty much like the past. This does not always turn out to be the case, of course, but if we can figure out—based on past behavior—what prices are most likely and then determine just how likely those most likely values are, then we’ll have something valuable.
A common way to do this is to look at average stock prices over some period together with how much they varied from the average. With this information, we can make some assumptions about where they are likely to be in the future.
Before we look specifically at the probabilities of stock prices, let’s look at an easy example of the general principles of probability. This example has to do with using two ordinary six-sided dice. Two dice are used in many games, including the gambling game of craps.
When we roll one die there are six possible values, one through six. Each value has an equal chance of coming up on each throw and that chance is one out of six.
When we throw two dice at once there are now six-times-six possible values for the total number of spots that end up facing up. Each one of the thirty-six combinations is equally likely if the dice are honest, but there are not thirty-six different possible two-dice totals because some totals can be thrown in more than one way.
Twelve (called Boxcars in craps) is not one of those totals that can be done in more than one way. There is only one combination that will do it. To roll a twelve we must have a six on the first die and a six on the second die. That one lone combination would only be expected to happen, on average, on one out of 36 throws.
Throwing a pair of fours, for a total of eight, also has only one chance of happening out of 36, but unlike the Boxcars combo for twelve, there are other ways to get a total of eight. In fact, we can identify exactly five separate ways to make a total of eight:
Die #1 Die #2
2 6
3 5
4 4
5 3
6 2
NEXT PAGE: What Are Gold Box Combinations?
|pagebreak|Each of these five combinations is equally likely to come up on any throw, so the chances of making a total of eight are five out of thirty-six. Rolling an eight is five times as likely as rolling a twelve.
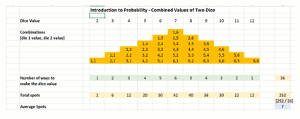
If we make a list of all the possible two-die totals that can be rolled, that list would look like the area in the gold boxes in the top of the figure below. For now, just focus on the gold boxes and the green row of totals below them:
In the area of the gold boxes, each column lists the separate combinations that add up the Dice Value number at the top of the column. In the column with 3 at the top, for example, there are two gold boxes: 1, 2 and 2, 1. Those are the only ways to make a three. That makes a total of two ways which is why “Number of ways to make the dice value” is 2 for this column. Reading across the green column, we can see that there is one way to make a 2, two ways to make a 3, three ways to make a 4 and so on. The more ways there are to make a number, the more times that number can be expected to come up in any long series of throws.
Now, let’s say that we throw the dice thirty-six times and record the results. Each separate combination comes up exactly once in those thirty-six throws. (By the way, this would virtually never actually happen with real dice throws. Each combination has a one-in-thirty-six chance of coming up on average on each throw).
From the stacks of gold boxes, we can see that the total of 7 has the most frequency, six out of thirty-six throws. The totals of 6 and 8 each have an average frequency of five out of thirty-six and so forth. The total of 7 is the most likely outcome on any individual throw, 6 and 8 are the next most likely, then 5 or 9, then 4 or 10, then 3 or 11, and finally 2 or 12, tied for last place.
Besides being the most likely total, 7 is also the average number of spots we will see. We can prove this by adding up all the spots on both dice for each throw and then dividing that total by 36, the total number of different possible throws. This is done in the yellow row labeled Total Spots. All the spots for all the throws add across the yellow row to 252. Dividing this total of spots by 36 throws, we get an average of exactly 7 spots per throw (the average throw is also the most likely throw). Values that are farther away from the average are less and less likely.
And, we can calculate just how much more or less likely any one throw is than any other throw. This will give us information we’ll need if we want to bet on the outcome of the dice.
That’s all the space we have for today but there is more to say about averages and probability. Before we close for today, I want to emphasize that stocks are not dice, they don’t move strictly at random. Even so, understanding their price history can give us ways to put parameters on possible future movement. More about that next time.
By Russ Allen, Instructor, Online Trading Academy