(03/09/15) Ask Not for Whom the Bell Curves

Options instructor Russ Allen, of Online Trading Academy, follows up the first part of his discussion on option probability with this today’s—also using the comparison of dice rolls—since being able to recognize when the price of options is unusual will help option traders identify opportunities to profit.

This is part 2 in a series on probability as it applies to option trading. The first part of it was discussed last Friday. You’ve probably figured out that the title is a word-play on the quote “Ask not for whom the bell tolls,” together with “the bell curve.”

If you’re searching your memory for where you’ve heard “for whom the bell tolls,” I’ll save you some time. You may have first encountered it in one of several places: For Whom the Bell Tolls was the title of a song by the heavy-metal band Metallica in 1984. This song was supposed to be a lyrical adaptation of a 1940 novel by Ernest Hemingway by the same title, set in the Spanish Civil War. That Hemingway book was made into a movie in 1943 and into two different TV miniseries in 1956 and 1965. According to Hemingway, he in turn got the title from a line in a poem by an English metaphysical poet named John Donne titled Meditation XVII, which was in a book published in 1624 called Devotions upon Emergent Occasions. That same poem also contained the phrase “no man is an island.”

So, now you know.

OK, so what is the bell curve part?

The bell curve, or bell-shaped curve, is another name for the so-called normal distribution curve. It is called the bell curve because of its shape. That’s easier to describe with a picture.

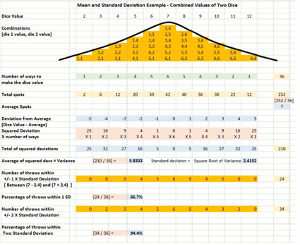
The first part of the figure below with the stacks of gold boxes from part one of this series. For now, don’t look down the diagram any further than the green row. In that first article, I described the possible outcomes from throwing two dice. With six faces on each die there are 36 possible two-die combinations and eleven possible 2-dice totals (2 through 12).

Each gold box in the figure below represents one of these 36 possible combinations and they are grouped into stacks under the two-dice total they add up to. The number of gold boxes in each stack is the number of times that dice value would be expected to come up, on average, per 36 throws. That count is shown below each stack in the row labeled, Number of Ways to Make the Dice Value. For the dice value of 3, for example, the Number of Ways is 2. This means that we’d expect, on average, to roll a three on two throws out of thirty-six throws.

We showed last week that the two-die total of seven was the most frequent total thrown and also the average value of all throws.

In the figure below, we’ve now superimposed a graph of the Number of Ways for each Dice Value. Once we connect those dots we get the graph shown by the heavy black line above the boxes. This line is vaguely bell-shaped, hence the name Bell Curve.

The bell shape of the curve, high in the middle and low on both sides, shows that more throws show up at the average (7) than at any other value; and that the farther from the average a value is, the fewer times we can expect to see it.

Click to Enlarge

[I should emphasize here that bell-shaped curves really only apply to phenomena whose nature is random, like dice throws. Any factor that has a non-random influence will cause the distribution to be different. If a corner on one of the dice is chipped, for example, then some values will come up more often than they otherwise would.]

We use averages to try to predict future outcomes. But besides the average of a set of values, it is important to know how widely those values tend to be dispersed around the average. If they diverge very little, then betting that the next event will be near the average will be a good bet. As the most extreme example, if one of our two dice had ones on all six faces and the other had all sixes, then every throw would be a seven with no deviation. We could predict with absolute certainty what the next throw would be every time. Betting on seven would be a sure bet. So, no one would ever take the other side of that bet and there would be no game.

NEXT PAGE: Is That Really How Real Dice Work?

|pagebreak|

But, that is not how real dice are. We do get different values and there is a way to evaluate how far apart those values tend to be. One of the most useful of these measures is the standard deviation. This tells us how far away from the average, on average, a typical result is. One important real-world application of this is to figure the average price of a stock and then to calculate how far away from that average the stock tends to range in a given period of time. If it tends to range far and wide, with lots of surprises, then its put and call options will be very expensive. If it tends to follow a straight and narrow path, then its options will be cheap.

But first back to the dice a final time to demonstrate the calculation of this standard deviation measure.

Each throw of the dice has a value between two and twelve. Each one of those values is different from the average or mean value, which is seven, by a certain amount. A throw of eight, for example, has a difference from the mean of 8 – 7 = 1. A throw of three has a difference of 3 – 7 = -4.

The standard deviation for all of the 36 possible throws is equal to: the square root of the average of the squared differences from the average value.

This seems like a lot of trouble; but that’s what computers are for. There are two reasons we square the differences and then “de-square” (take the square root of) the average difference rather than just averaging the differences:

This gets around the problem that some of the differences are negative numbers. If we simply averaged the differences they would average out to zero. But when we square each difference the result is a positive number and these can then be averaged.
Doing this gives us a larger number for standard deviation when values are widely spread out, even if they’re spread evenly on each side of the average. If we just averaged the absolute value of the differences this would not be the case.

In the table, the rows beginning with the blue row step through this calculation. First, in the blue row each throw’s difference from the average is shown. For a Dice Value of two, the difference is 2-7 = -5. For a Dice Value of three, it’s 3-7 = -4, and so on.

Next we have to square those differences. This is done in the orange row labeled Squared Deviations.

Now we have to average those squared deviations. To do this we have to take the squared deviation from the first orange row and multiply it by the number of ways that Dice value can be made, then add up these totals. This is done in the blue row, labeled Total of Squared Deviations. The total of the squared deviations is 210. Dividing this total by 36 (the total number of throws and also the total of the Number of Ways) gives the average of the squared differences, which is 5.833. This number is called the variance for this data set.

Finally, we take the square root of the variance and get 2.415 as the standard deviation.

The last two gold rows in the table tell us how often we would expect to see a Dice Value that is less than one standard deviation away from the average and less than two standard deviations away respectively.

A value within one standard deviation of the average would be 7 plus or minus 2.415, or from 4.585 to 9.415. This would include dice values of 5 through 9, but not 2,3,4,10,11 or 12. Altogether, 24 out of 36 throws would be expected to be in this range. That’s 66.7%.

A value within two standard deviations of the average would be 7 plus or minus (2 * 2.415), or from 2.170 to 11.83. This would include all dice values except 2 and 12. Eliminating these 2 throws leaves 34 of the 36 of the possibilities within two standard deviations. That’s 94.4%.

These two percentages (67% of results within one standard deviation and 94% within two standard deviations) are typical of what we see in random, or normal (in the mathematical sense) distributions of things. With larger populations than just these 36 throws, so that the results are more granular, the percentages are close to 68% within one standard deviation and 95% within two.

Wow. I’m sure that that is far more than you wanted to know about bell curves, averages, and standard deviations. The main takeaways are: