Citing an example for support, options instructor Russ Allen, of Online Trading Academy, explores the limited-risk option trading strategy with lower margin requirements known as the Iron Condor.
One of the more interesting option strategies is the Iron Condor. This one takes advantage of situations where we expect a stock to stay within a range for a while and where its options are richly priced.
The general idea is that we can sell options with strike prices outside the range where we expect the stock to stay. We get paid well for selling them, and if all goes well, they dry up and blow away (expire worthless). In case we read it wrong, however, we buy ourselves some insurance to limit our risk.
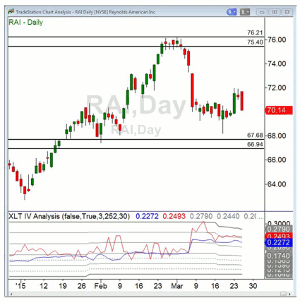
A case in point was Reynolds American Inc. (RAI), as shown on this chart:
The stock was fairly near the middle of a range, between a solid demand zone near $75 and a strong supply zone near $67 which we expected to contain it at least for a few weeks. Its options were pretty highly inflated, showing implied volatility of 25%. This was compared to a one-year range for IV that stretched from 12% to 30%.
Our plan was to sell put options at a strike price below the demand zone at the $65 strike and also sell call options at a strike near the supply zone at $75. We used options from the April expiration, 22 days away. We expected these options to become worthless, leaving us to keep the premiums we received for selling them. That premium totaled $1.20 per share.
In case we got a nasty surprise in the form of a big move beyond either of our short option strike prices, we bought options at strike prices even farther away. These would be our insurance. We decided on the $60 puts and $80 calls, each one’s strike or $5 beyond our short strikes. These two insurance options together cost us $.50 per share out of our $1.20 proceeds, leaving us with a $.70 net credit per share, or $70 per 100-share contract.
With the addition of the insurance options, our maximum loss was reduced greatly. In the worst case, on the upside, the stock could shoot up past our upper call strike of $80. If so, the short call at the $75 strike would be deeply in-the-money. But our long $80 call would then also be in-the-money and we would have no further losses once that $80 strike was reached. The difference between the values of the two options could never be more than $80-75 = $5, so that $5.00 per share is the most we would have to pay to exit the trade. Subtracting our net credit of $.70, our maximum loss was $4.30.
Similarly on the downside, our worst case would be having to pay $5 to exit the trade if the stock dropped below our $60 long put strike. This would also result in a net loss of $4.30 per share.
NEXT PAGE: The Limited-Risk Trade
|pagebreak|A side benefit of buying these insurance options was that they reduced our capital requirement greatly. To sell the $65 put and $75 call without insurance would have required at least 20% of the underlying price as margin and even more at some brokers. This would have amounted to about $14 per share, rather than $4.30. The reason for the high margin requirement was that—without the insurance—both short options would be naked, and therefore, have theoretically unlimited risk. We would have planned to mitigate this risk by putting in stop-loss orders to liquidate the trade if the stock passed our boundaries, but brokers don’t consider stop-losses when calculating margin requirements for option trades.
With the insurance options, the trade became an Iron Condor. This is a limited-risk trade, and as such, has lower margin requirements. The most that we would be required to keep on deposit to secure this trade would be the $5 per share maximum liability. We received $.70 credit to enter the trade, leaving us to use $4.30 of our own money.
The return of $.70 on $4.30 was over 16% in just 23 days. This amounts to an annualized return too high to bother to calculate.
But wait, you’re saying: how can it make sense to risk $4.30 to make $.70? The answer is that it can make sense if the probabilities are strongly in your favor, as they were here.
In order for the trade not to make its maximum profit, one of our short options would have had to end up in-the-money. For that to happen, the stock would have had to go either above our $75 short call strike or below our $65 short put strike. We did not find this likely because of our chart analysis.
We could also use our analysis tools to get some statistical confirmation of the unlikelihood of RAI moving past our strike prices. One of these tools is the “Probability of expiring out-of-the-money” indicator in the TradeStation platform. Some other trading platforms provide similar tools.
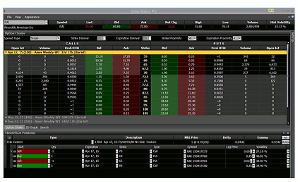
Below is the RAI option chain with the Prob OTM column activated:
The probability of the $65 put finishing out-of-the-money was given as 94%. The probability for the $75 call was a little less, at 84%, still plenty high.
So, on the low side there was only a 100-94 = 6% probability of our $65 put costing us any money; and on the high side a 16% chance that our short $75 call would do so. This is an exercise in conditional probability, if the stock was above $75 there was zero probability of it also being below $65. So, the total chance of not making our maximum profit was not the combination of the two options (14% + 6%). Instead, it was the higher of the two possibilities or 14%.
The probabilities of our actually incurring the maximum $4.30 loss were even tinier. The probability of the $80 call finishing out-of-the-money was given at 98.5% and the $60 put at 99.9%.
All in all, this looked to be an attractive trade. Our statistical tools gave us good confirmation of what the price chart told us in the first place. We would never take a trade based on the statistical probabilities alone because that’s just what they, probabilities, not certainties. But when used in combination with proper supply and demand chart analysis, they give us powerful backup.
By Russ Allen, Instructor, Online Trading Academy