Much like a casino, in trading, there is a "house." The house, in this case, is the liquidity provider, or market maker. Each trade a market maker makes may be a winner or a loser. But because market makers can buy the bid and sell the offer, they have a statistical edge over the "retail" trader; they buy at a cheaper price and sell at a higher price. So, where does that leave the retail trader? Retail traders must find a way to gain edge themselves.
An important influence on a retail trader's edge is vega-one of the option greeks. Vega is the rate of change of an option's value relative to a change in implied volatility. To understand vega, let's get better acquainted with the concept of volatility.
Options and Volatility
Option values have
three main influences: the price of the underlying, time to expiration, and
volatility. The influence of the price of the underlying is fairly intuitive to
even novice option traders. As the stock or index price rises, calls rise and
puts decline. As the stock or index falls, calls decline and puts rise. These
changes in option value due to direction are measured by the option greek
delta.
The effect of time is a relatively easy to grasp concept as well. If you bought an option for, say, $2, would you rather it has one week till expiration or one year? Clearly (all else held constant) the more time your option has to expiry the better. Therefore, as time passes, options lose value (again, all other factors held constant). This change is measured by theta.
But the trickier and (arguably) more useful pricing factor for gaining in the effects of edge is that of volatility. The volatility of stock price movement can be measured by the stock's standard deviation. Typically, this figure is annualized for comparison purposes. The annualized standard deviation of a stock is often referred to as realized volatility. This figure is stated as a percentage of the stock's price. A typical realized volatility figure is generally between 10 percent and 50 percent-10 percent being not very volatile and 50 percent being fairly volatile-though the figure can be above or below that range, even significantly. The bigger the realized volatility percentage, the bigger the stock's price swings have been lately.
Volatility is a factor of option prices. When the market expects volatility to be high, upward price pressure is put on options as hedgers and speculators create demand. Likewise, when traders bank on lower volatility, hedgers and speculators freely supply the market with options putting downward pressure on prices. In this context, volatility is called implied volatility. Implied volatility is the volatility component of an option's price.
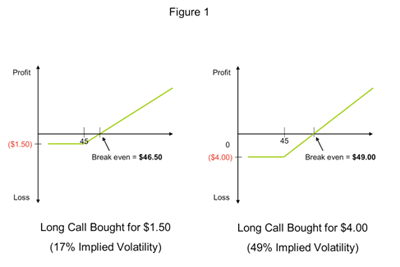
Imagine two scenarios: In both situations the underlying stock pays no dividend and is trading at $45 a share. In Scenario 1 the January 45 call is trading at $1.50, and in Scenario 2, the January $45 call is trading at $4.00. Why are the two otherwise identical calls different? Implied volatility. The January 45 calls in Scenario 1 have an implied volatility of around 17 percent, and the implied volatility for the calls in Scenario 2 is about 49 percent. Big difference.
In either case, a clever trader can compare the implied volatility of the options with the realized volatility of the stock. That is, given a particular realized volatility figure, the trader can compare the actual stock volatility with the volatility implied by its options. This is one measure traders look at to gauge the relative expense of options.
So, the real question is: How does this help edge?
Imagine the same two scenarios as mentioned above. Now consider the "price" of the options as measured by implied volatility if the realized volatility of the underlying stock is 25 percent. The calls in Scenario 1 are priced lower than the volatility of where the stock is trading. The calls in Scenario 2 are priced higher than the realized volatility.
Consider, then, a trader interested in buying a January 45 call because he believes the stock will rise (i.e., it is underpriced). How did the trader arrive at such a forecast? It is likely he considered several indicators from a technical analysis perspective in conjunction with a fundamental analysis. Why several technical indicators and a fundamental review? To give him the maximum chance of success-or edge-directionally.
If this trader is smart, he will also examine the option's price in terms of volatility. Volatility is, after all, a component of its price; it is one of the things the trader is considering buying. He will take note of whether the option is overpriced or underpriced in terms of implied vs. realized volatility.
We can take some of the mystique out of implied volatility by considering the call purchase graphically. Figure 1 shows two simple at-expiration P&(L) diagrams for the calls in the two different volatility scenarios.
Clearly the call purchased in the higher implied volatility scenario ($4.00) is at a disadvantage compared with the one bought for the lower implied volatility ($1.50). The disadvantage is that the underlying stock must rise much more for the option to break even at its expiration. To point out the obvious, it is more advantageous to buy less expensive options. But these diagrams point out that the difference is due to the implied volatility level at which the option is initially purchased. Directionally speaking, as the underlying stock moves lower, the 49 percent volatility option will lose more by expiration. As the underlying rises, it needs to rise more for the 49 percent option to make up for the relatively more expensive premium. The best way to truly gauge the relative cheapness or expensiveness of the option-barring directional considerations-is to look at the implied volatility.
Caveat
There is, however, one more thing to
consider. If implied volatility is higher than realized volatility, it may be
because the market expects the future volatility of the underlying stock to be
higher than it has been lately (i.e., realized volatility). The market,
therefore, would "price in" higher future volatility into the price of the
options. Remember, using realized and implied volatility can help a trader gain
edge, but it cannot guarantee success.
Dan Passarelli is the author of the books Trading Option Greeks and The Market Taker's Edge. Dan is the founder and CEO of Market Taker Mentoring LLC (http://markettaker.com), which provides education to option traders. Dan can be reached at dan@markettaker.com.
Options involve risk and are not suitable for all investors. Before trading options, please read Characteristics and Risks of Standardized Option (ODD) which can be obtained from your broker; by calling (888) OPTIONS; or from The Options Clearing Corporation, One North Wacker Drive, Suite 500, Chicago, IL 60606. The content n this article is intended to be educational and/or informative in nature. No statement is intended to be a recommendation or solicitation to buy or sell any security or to provide trading or investment advice. Traders and investors considering options should consult a professional tax advisor as to how taxes may affect the outcome of contemplated options transactions.