Deep out-of-the-money puts that trend in your direction can be rolled to extend profits, but be careful not to add risk, notes Alan Ellman.
After selling an out-of-the-money (OTM) cash-secured put and then stock price accelerates substantially, the put value will decline. Share price and put value are inversely related. This allows us to take advantage of our 20% over 10% put-selling exit strategy guideline. With this exit strategy, if we can retain 80% to 90% of our original option credit mid-contract, we close our short put and use the newly freed up cash to secure a new put with a different underlying security.
In April 2019, Haltore, a subscriber, wrote to me regarding a put he was in with Nvidia Corp. (NVDA). After entering the trade, NVDA moved up in price and Haltore was considering rolling up to a higher strike with the same expiration date. This would result in an additional option credit. The question he posed was is this a viable exit strategy maneuver?
Haltore’s trade with NVDA AS OF April 16, 2019
- March 29, 2019: With NVDA trading at $177.25, Haltore sold the Jan. 17, 2020 $155.00 OTM put for $12.07 (a LEAPS option was sold)
- April 16, 2019: With NVDA is trading at $187.42 Haltore is considering closing the $155 put and opening a $175 put expiring on the same date for an additional option credit
Initial trade structuring using the BCI Put Calculator (below)
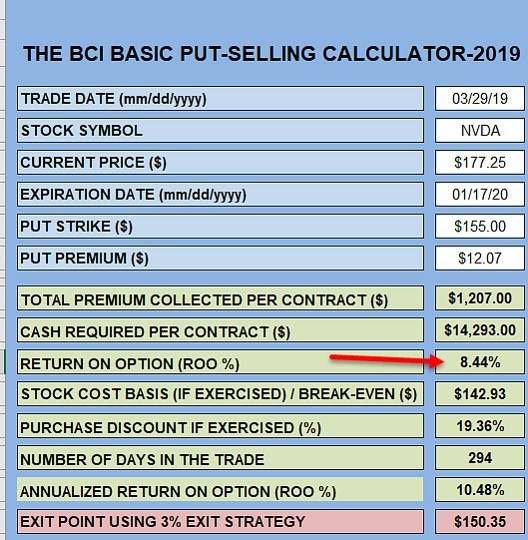
The red arrow above highlights the 294-day 8.44% initial time value return. With the stock currently trading at $187.42, the maximum return is looking good. The question is, should we roll up to a higher strike to generate an even higher return?
Option chain to roll up from the $155 strike to the $175 strike (Jan. 17, 2020 expiration)
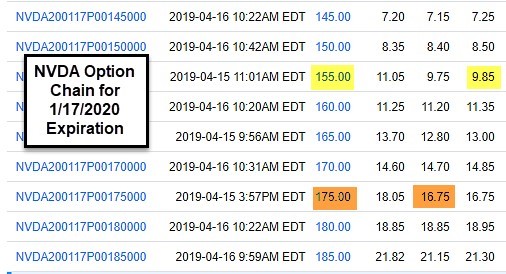
Rolling up results in an option credit of $6.90 ($16.75 – $9.85) so why not pull the trigger? Well. One there will be additional capital required to execute the second trade. Brokers will require cash to secure these puts using the following formula: (put strike – put premium) x 100 per contract.
This comes to $14,293 for the $155 strike but the higher strike will require more capital:
($175.00 – $16.75) x 100 = $15,825.00 or an additional $1532.00 per contract
The breakeven for this trade moves up creating more risk:
The breakeven is the (put strike – the put premium) x 100 per contract.
For the $155 strike the breakeven is $155.00 – $12.07 = $142.93
For the $175.00 strike the breakeven is $175.00 – 16.75 – $158.25, more than $15.00 higher.
Is there a better way to enhance results?
Consider selling shorter-term option, like monthlies. If we annualize monthly options versus longer-term expirations, we will win every time. Let’s view the option chain for the $175.00 one-month out
VDA put (below).
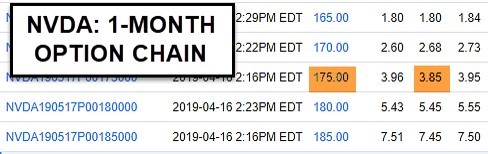
AS you can see, the one-month option generates $3.85 or a 2.2%, one-month return. This annualizes to 26.4% compared to the 10% annualized return that the original 10-month 8.4% return originally offered.
Discussion
Rolling up a deep OTM puts will add an additional option credit but will require additional cash for the trade and additional risk as the breakeven price rises. Monthly options will offer greater annualized returns than longer-term options in addition to allowing us to re-assess our bullish assumption on the stock more frequently.
Use the multiple tab of the Ellman Calculator to calculate initial option returns (ROO), upside potential (for out-of-the-money strikes) and downside protection (for in-the-money strikes). The breakeven price point is also calculated. FREE Beginner’s Corner Tutorial for Covered Call Writing has Been Enhanced and Updated here:





















