While a number of factors weigh on option pricing, studying the element of time decay, or Theta, is a crucial starting point for option traders, particularly when selling premium, says John Summa of Investopedia.com.
Most investors and traders new to options markets prefer to buy calls and puts because of their limited risk and unlimited profit potential. Buying puts or calls is typically a way for investors and traders to speculate with only a fraction of their capital. But these straight option buyers miss many of the best features of stock and commodity options, such as the opportunity to turn time-value decay into potential profits.
When they establish a position, option sellers collect time-value premiums paid by option buyers. Rather than struggling against the ravages of time value, the option seller can benefit from the passage of time and time-value decay becomes money in the bank even if the underlying is stationary.
For option writers (sellers), time-value decay thus becomes an ally instead of a foe. If you have ever sold covered calls against stock positions, you can appreciate the beauty of selling time value.
In this article, I focus on the importance of time value in the option-pricing equation. But before turning to a detailed look at the phenomena of time value and time-value decay, let's review some basic option concepts that will make it easier for you to understand what we mean by time value.
Options and Strike Price
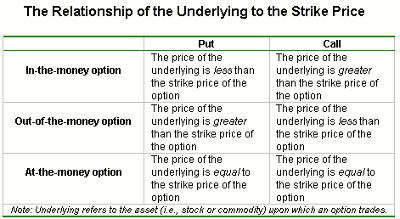
Depending on where the underlying price is in relation to the option strike price, the option can be in-, out-, or at-the-money. Let's look at this relationship while keeping in mind our central focus on time value.
When we say an option is at-the-money, we mean the strike price of the option is equal to the current price of the underlying stock or commodity. When the price of a commodity or stock is the same as the strike price (also known as the exercise price), it has zero intrinsic value, but it also has the maximum level of time value compared to that of all the other option strike prices for the same month.
Figure 1 below provides a table of possible positions of the underlying in relationship to an option's strike price.
As can be seen in Figure 1, when a put option is in-the-money, the underlying price is less than the option strike price.
For a call option, in-the-money means that the underlying price is greater than the option strike price. For example, if we have an S&P 500 call with a strike price of 1100 (an example we will use to illustrate time value below) and if the underlying stock index at expiration closes at 1150, the option will have expired 50 points in-the-money (1150 - 1100 = 50).
In the case of a put option at the same strike price of 1100 and the underlying at 1050, the option at expiration also would be 50 points in-the-money (1100 -1050 = 50).
For out-of-the-money options, the exact reverse applies. That is, to be out-of-the-money, the put's strike would be less than the underlying price and the call's strike would be greater than the underlying price.
Finally, both put and call options would be at-the-money when the strike price and underlying expire at the exact same price. While we are referring here to the position of the option at expiration, the same rules apply at any time before the options expire.
NEXT PAGE: Time Value of Money
|pagebreak|Time Value of Money
With these basic relationships in mind, let's now take a closer look at time value and the rate of time-value decay (represented by Theta, from the Greek alphabet).
If we leave volatility aside for now, the time-value component of an option, also known as extrinsic value, is a function of two variables:
- Time remaining until expiration, and...
- The closeness of the option strike price to the money
All other things remaining the same (i.e. no changes in the underlying and volatility levels), the longer the time to expiration, the more value the option will have in the form of time value. But this level is also affected by how close to the money the option is.
For example, two call options with the same calendar month expiration (both having the same time remaining in the contract life) but different strike prices will have different levels of extrinsic value (time value). This is because one will be closer to the money than the other.
Figure 2 below illustrates this concept, indicating when time value would be higher or lower and whether or not there will be any intrinsic value (which arises when the option gets in-the-money) in the price of the option.
As Figure 2 indicates, deep-in-the-money options and deep out-of-the-money options have little time value. Intrinsic value increases the more in the money the option becomes. And at-the-money options have the maximum level of time value but no intrinsic value.
Time value is at its highest level when an option is at-the-money because the potential for intrinsic value to begin to rise is the greatest right at this point.
Time-Value Decay
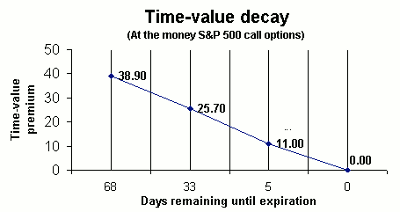
In Figure 3 below, we simulate time-value decay using three at-the-money S&P 500 call options, all having the same strikes but different contract expiration dates. This should make the above concepts more tangible.
Through this presentation, we are making the assumption (for simplification) that implied volatility levels remain unchanged and that the underlying is stationary. This helps us to isolate the behavior of time value. The importance of time value and time-value decay should thus become much clearer.
Taking our series of S&P 500 call options, all with an at-the-money strike price of 1100, we can simulate how time value influences an option's price.
Assume the date is February 8. If we compare the prices of each option at a certain moment in time, each with different expiration dates (February, March, and April), the phenomenon of time-value decay becomes evident. We can witness how the passage of time changes the value of the options.
Figure 3 graphically illustrates the premium for these at-the-money S&P 500 call options with the same strikes. With the underlying stationary, the February call option has five days remaining until expiry, the March call option has 33 days remaining, and the April call option has 68 days.
As Figure 3 shows, the highest premium is at the 68-day interval (remember prices are from February 8), declining from there as we move to the options that are closer to expiration (33 days and five days).
Again, we are simply taking different prices at one point in time for an at-the-option strike (1100) and comparing them. The fewer days remaining translates into less time value. As you can see, the option premium declines from 38.90 to 25.70 when we move from the strike 68 days out to the strike that is only 33 days out.
The next level of the premium, a decline of 14.70 points to 11, reflects just five days remaining before expiration for that particular option. During the last five days of that option, if it remains out-of-the-money (the S&P 500 stock index below 1100 at expiration), the option value will fall to zero and this will take place in just five days. Each point is worth $250 on an S&P 500 option.
One important dynamic of time value decay is that the rate is not constant. As expiration nears, the rate of time-value decay (Theta) increases (not shown here). This means that the amount of time premium disappearing from the option's price per day gets greater with each passing day.
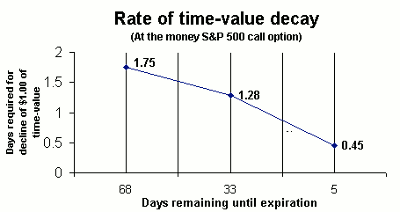
The concept looked at in another way in Figure 4, the amount of days required for a $1 (1 point) decline in premium on the option will decrease as expiry nears.
Looking at the exhibit, you can see that at 68 days remaining until expiration, it takes 1.75 days for a one-dollar decline in premium. But at just 33 days remaining until expiration, the time required for a one-dollar loss in premium has fallen to 1.28 days.
In the last month of the life of an option, Theta increases sharply and the days required for a one-point decline in premium falls very fast. At five days remaining until expiration, the option is losing one point in just less than half a day (.45 days).
If we look again at Figure 3, at five days remaining until expiration, this at-the-money S&P 500 call option has 11 points in premium. This means that the premium will decline by approximately 2.2 points per day. Of course, the rate increases even more in the final day of trading, which we don't show here.
Bottom Line
While there are other pricing dimensions (such as Delta, Gamma, and implied volatility), a look at time-value decay is a good place to start when beginning to understand how options are priced.
By John Summa, CTA, PhD, contributor, Investopedia.com
John Summa is also the founder of Hedge My Options