Matthew Kerkhoff, options expert and editor of Dow Theory Letters, continues his 14-part educational series on understanding options and their role in investment portfolios. This series will run each Friday on MoneyShow.com through December, moving from the basics through increasingly more sophisticated strategies.
In the last part of our ongoing options series, we began to dive into actual option strategies by discussing how to purchase portfolio “insurance.” Today we’re going to discuss how to close out this type of position, and we’re also going to explore some of the factors that affect the pricing of options.
If you missed any of the prior five prior segments, they can be found below:
Part 1 and 2: Understanding Put Options
Part 3: Understanding Put Options
Part 4: Factors that Affect Options Prices
Part 5: Portfolio Insurance (Part 1)
Now, let’s continue with our exploration of portfolio insurance and check in on how our hypothetical position that we established last month is doing.
To refresh your memory, under the guise of a richly valued market with substantial geopolitical risks, we decided to protect our portfolio by purchasing put options.
In our example from last month, we decided to purchase a put option on SPY that expires on May 19th and has a strike price of $236. For this, we paid a premium of $335 per contract.
Roughly one month has passed since then, so let’s check in and see what the value of our put option is.
The table below shows the current pricing for SPY puts that expire on May 19th. The specific contract that we purchased ($236 strike price) is highlighted in orange.
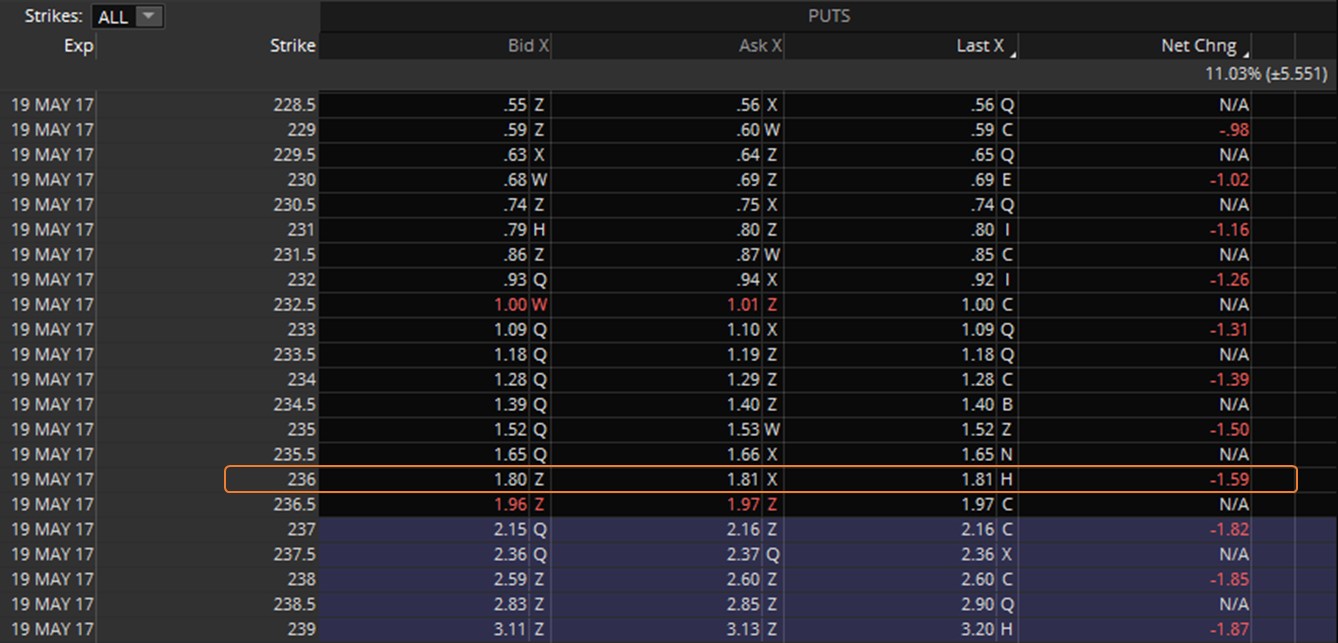
As you can see, the current price of our put option is now about $180. Considering that we paid $335 for this option contract last month, we currently have a loss of approximately $155.
Why is this?
Generally speaking, the biggest driver of option prices is the value of the underlying security – in this case SPY. Right now (after this morning’s 1% pop), SPY is currently trading at $236.91.
Because the current price of SPY is above our put option contract’s strike price of $236, this option currently holds no “intrinsic value.” Intrinsic value is a term used to describe the value an option would have if it were exercised today.
At the moment, exercising our $236 put option would not make sense because why would we sell our shares of SPY for $236 when we could sell them in the market for more than that ($236.91)? Because there is no value to be gained by exercising our option right now, this option is said to have no intrinsic value.
As a quick example to highlight the alternate scenario, let’s say SPY was currently trading at $235 per share. If that were the case, then our put option would have an intrinsic value of $1. (There is $1 of value to be gained per share if we were to exercise the option immediately.)
All option prices are made up of two components. Intrinsic value is one of these components, and the other is called time value (I’ll explain this momentarily).
In equation form, we would see the relationship like this:
FREE 14-part guide to options: The Basics to In-Depth Portfolio Strategies
Option premium (price) = Intrinsic Value + Time Value
This relationship is important to understand because as we get into more complex option strategies, separating out intrinsic value from time value is going to be very important.
Getting back to our example, since we know that the intrinsic value of our option contract is zero, we can quickly figure out the time value component. Rearranging our equation above, we see that:
Time Value = Option premium (price) – Intrinsic value
If we take the current price of our option contract ($1.80) and subtract the intrinsic value component ($0) we are left with a time value of $1.80. Said differently, our put option contract’s price is comprised entirely of time value.
So what exactly is time value?
Time value represents the amount of time an option position has to become profitable due to a favorable move in the underlying’s price (in this case SPY).
Because our option contract does not expire until May 19th, we still have 25 calendar days left in which SPY could drop below $236, at which point the intrinsic value of our option would begin to rise.
Time value, as you might expect, is a function of how much time is remaining until expiration, and it “decays” over time. As the expiration date approaches, the time value component of our option will go to zero.
Here’s a quick chart showing how time value behaves over time. Pay special attention to the fact that time value decay does not occur in a linear fashion, but rather exponentially. That is, time decay tends to accelerate as the expiration date approaches.
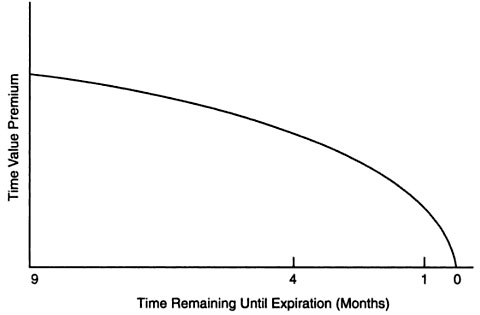
This exponential decay of time value is going to come into play in future option strategies, because in many instances the best way to make money from options is to allow time decay to work in our favor (i.e. be a seller of options). In these scenarios, we’re going to want to target options where time decay occurs the fastest (near expiration).
Getting back to our example, if the share price of SPY were to remain unchanged until May 19th, we would see the value of our put option decline from $1.80 today to zero at expiration. In this scenario, our option is said to have expired worthless. In a sense, we would have paid for an insurance policy that we didn’t need to use.
But as holders of this portfolio insurance, we have other options at our disposal. In fact, one of the great aspects of using options as portfolio insurance is that we can exit our position at any time.
Let’s say that one of our big worries (and reasons for holding this portfolio insurance) was the French elections that occurred yesterday.
With that temporarily out of the way and the markets responding favorably, perhaps we no longer feel the need to have our portfolio insured. If this was the case, we could exit the position today, selling our put option back into the market for $180.
As you’ve probably surmised, option prices change on a second by second basis just like stock prices. These adjustments to the premium (price) reflect changes in the intrinsic value and time value of each option.
As an example, notice in the top chart that the net change (change from yesterday’s closing price) of our put option is $-1.59. This means that yesterday, our put option was worth roughly $3.39 ($1.80 + $1.59) -- a bit more than we paid for it initially. So what’s responsible for the big drop in price?
If we look at the underlying (SPY), we can see that SPY is currently trading $2.32 higher today than the price at which it closed yesterday. At yesterday’s closing price of $234.59, our option actually had an intrinsic value of $1.41 ($236 - $234.49).
If we take that $1.41 (the intrinsic value component) and subtract it from yesterday’s put option price of $3.39, we get a time value component of roughly $1.98. That’s how things stood at the close on Friday.
But because of today’s jump in price, all the intrinsic value of our option disappeared, leaving only time value. And not only that, but since additional days passed and there is less time remaining until expiration, the time value component of our option eroded, leaving our option worth the $1.80 we see today.
This interplay between intrinsic value and the decay of time value is occurring all the time. We’re going to get into more of the factors that affect the time value component in future articles, but I think we’ve covered enough for today.
In closing, I want to go through one final example scenario to highlight how we would exit this position in the event we were ultimately correct, and SPY suffered a big drop.
Let’s say that over the next 25 days SPY falls to $220 per share. Can you determine what the value of our put option would be?
At expiration, we know that the time value component of our put option’s price would have gone to zero. In that case, the entire value of our option would come down to its intrinsic value. With a share price of $220, our put option (which has a strike price of $236) would be worth $16 ($236 - $220). And because each option contract again represents 100 shares, it means that this put option would have $1600 worth of value.
At this point, we would have two options. We could allow our put option to be exercised, which would result in us actually selling 100 shares of SPY at $236 per share to whoever sold us our put option (and we could then use the proceeds to repurchase 100 shares of SPY in the market at $220 per share -- reestablishing our position), or we could simply sell our put option back into the market for the $1600. In either scenario, we are capturing the value that was lost in our original insured position (the $16 per share loss that occurred).
In most cases, assuming that we want to maintain our original position, we’re going to want to simply take the profit on the option trade. If we did this, the $1600 loss that our stock portfolio took would be offset by the $1600 in premium we received from our put option. We would still be out our original premium that we paid (the $335) but we would have effectively protected our portfolio from a substantial decline.
This wraps up our discussion on portfolio insurance, but we will revisit this topic as we continue further into the world of options. At this point, don’t be stressed if your grasp on all this stuff is still fuzzy. As you get more used to the terminology, reading though these articles and examples will become easier and easier.
In the next installment in this series, we’re going to look at how to rent out your stocks (or ETFs) to generate extra income. This is an especially important topic considering today’s low rate environment and elevated valuation levels … so stay tuned.





















