How to Hedge a Stock or ETF Position with Options

In this article, I will discuss a concept that is somewhat vague to many novice traders. First, I will define Delta in the most traditional way, and then I will provide an example of using Delta as a hedge.

Part One: Definition

Prior to elaborating on Delta, I will first define it and give some of its basics. The Delta of any option is expressed in a percentage amount, yet the actual percentage sign is generally omitted when quoting the Deltas. The Delta represents the change in the option price (premium) given a one-point change in the price of the underlying issue. I purposely use the word "issue" rather than the word "stock" because it is all-inclusive. The issue could stand for any of the underlying assets: Commodities, futures, stocks, indices, or ETFs (exchange traded funds).

The call premium will increase when the underlying issue's price increases, whereas the put premium decreases during an uptrend. A quick disclaimer: In this example, I am assuming that all other things are equal, and I am taking IV (implied volatility) fluctuation out of the equation.

The put premium will increase when the underlying issue's price drops, whereas the call premium decreases during a downtrend. Moreover, puts that are out of the money (OTM) will have small Deltas, while a deep-in- the-money (ITM) put will move very close to the same amount as the underlying, only in the opposite direction. The puts go up in value when the underlying drops. Deep ITM puts have Deltas that are close to negative one. Those that are at the money (ATM) have a value of approximately -0.5, etc.

Part 2: A Hedge Example

In my classes, for educational purposes, I often take a long equity position with a hundred shares on any of the stocks. As soon as I get filled, I ask the option students what is my current Delta. Most of the time, they look at me full of surprise that I am asking about an option Greek when the only open position is the 100 shares of stock.

Once the confusion passes, the realization emerges that 100 long shares of the stock gives a Delta of 100. Next, I ask the students what amount of Delta I would have if I had shorted the stock with 100 shares. This time, the pause between my question and their answer is much shorter, for the answer is still the same. The only difference is that in the case of a short position, there is 100 Delta, but they are negatively correlated.

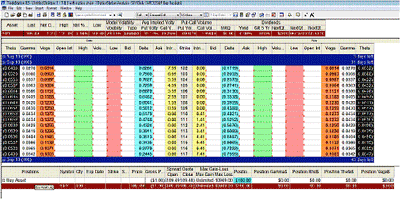
In the chart below, I have colored the Deltas in a light blue color and placed them in between their respective bid and ask prices for the calls and puts on the option chain. The TradeStation platform's option analysis window has four components, and Figure 1 displays only three of them. The Asset Pane and Position Pane are highlighted in brown, and what I have done is simply insert a theoretical position long 100 SPY. In turn, that has produced 100 long Deltas. What this means in layman's terms is that if the stock goes up, the underlying asset/issue, in our case the exchange traded fund SPY, will move penny for penny in the direction of SPY.

Figure 1
Click to Enlarge

Next, let me move to the specification of how to hedge that long SPY position of 100 shares. In my previous articles, I have suggested how to select a put strike price based on where the equity trader would place the stop loss. At the time of writing this article (August 17, 2010), the average true range of SPY on a weekly basis is $5.15. Hence, if the trader wants to be protected, then a minimum of six points of breathing room is needed. The current price of SPY is $109.47, and protection could be placed at the 103 strike price. This 103 put is more than six points away from the price of the underlying (109.47 - 103), which is also greater than 5.15, the natural weekly vibration/fluctuation of SPY.

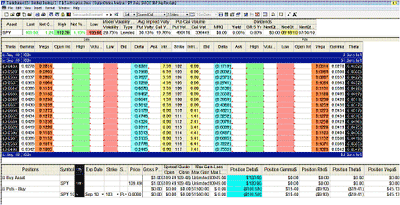
Nevertheless, the Delta of the 103 put is -0.2032, so in order to hedge all 100 shares, we must get five contracts. Observe on Figure 2 that five puts were bought, which produced an aggregate of (five times 0.2032) 100 negative Deltas, and a bit more. So what we have in the position pane (colored in black background) is the quantity of 100 long shares of SPY, and on the line below, the five contracts of the long puts. This together hedges our position and makes it neutral. If SPY drops below 103, we are protected, but if SPY goes higher, the underlying would be making a profit while the value of the put would be losing value.

Figure 2
Click to Enlarge

In conclusion, in this article, I have first given the simple definition of the mostly widely used Greek component, and then have proceeded with an explanation of using Delta as a hedge. There is so much more to the Greeks than what meets the eye, so I suggest constant learning and expanding of option knowledge. Trade options wisely based on your intricate knowledge of them.