(09/02/09) Synthetic Put and Call Spreads Made Easy (Part 2)

Married Put (Continued)

So if the married put is a more expensive endeavor than the long call because of the interest paid on the investment portion that is below the strike, why would anyone buy a married put? Wouldn’t traders instead buy the less expensive—and less capital intensive—long call?

Given the additional interest expense, they would rather buy the call. This relates to the concept of arbitrage. Given two effectively identical choices, rational traders will choose to buy the less-expensive alternative. The market as a whole would buy the calls, creating demand that would cause upward price pressure on the call. The price of the call would rise until its interest advantage over the married put was gone.

In a robust market with many savvy traders, arbitrage opportunities don’t exist for very long. It is possible to mathematically state the equilibrium point toward which the market forces the prices of call and put options by use of the put/call parity. The put/call parity equation states:

c + PV(x) = p + s where

c is the call premium
PV(x) is the present value of the strike price
p is the put premium
s is the stock price.

Another less academic and more trader-friendly way of stating this equation is:

Call + Strike – Interest = Put + Stock …

…where Interest is calculated as:

Interest = Strike x Interest Rate x (Days to Expiration/365)

The two versions of the put/call parity stated here hold true for European options on non-dividend-paying stocks.

Dividends

Another difference between call and married put values is dividends. A call option does not extend to its owner the right to receive a dividend payment. Traders, however, who are long a put and long stock are entitled to a dividend if it is the corporation’s policy to distribute dividends to its shareholders.

An adjustment must be made to the put/call parity to account for the possibility of a dividend payment. The equation must be adjusted to account for the absence of dividends paid to call holders. For a dividend-paying stock, the put/call parity states:

Call + Strike – Interest + Dividend = Put + Stock

The interest advantage and dividend disadvantage of owning a call is removed from the market by arbitrageurs. Ultimately, that is what is expressed in the put/call parity. It’s a way to measure the point at which the arbitrage opportunity ceases to exist. When interest and dividends are factored in, a long call is an equal position to a long put paired with long stock. In options nomenclature, a long put with long stock is a synthetic long call. Algebraically rearranging the above equation:

Call = Put + Stock – Strike + Interest – Dividend

The interest and dividend variables in this equation are often referred to as the basis. From this equation, other synthetic relationships can be algebraically derived, like the synthetic long put.

Put = Call – Stock + Strike – Interest + Dividend

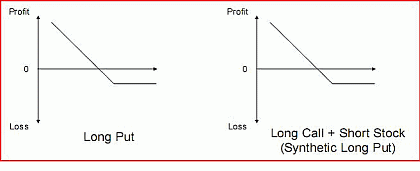
A synthetic long put is created by buying a call and selling (short) stock. The at-expiration diagrams in FIGURE 6.2 show identical payouts for these two trades.

Figure 6.2 Long Put vs. Long Call + Short Stock

Click to Enlarge

Synthetics

The concept of synthetics can become more approachable when studied from the perspective of delta as well. Take the 50 strike put and call listed on a $50 stock. A general rule of thumb in the put-call pair is that the call delta plus the put delta equals 1.00 when the signs are ignored. If the 50 put in this example has a –0.45 delta, the 50 call will have a 0.55 delta. By combining the long call (0.55 delta) with short stock (–1.00 delta), we get a synthetic long put with a –0.45 delta, just like the actual put.

The directional risk is the same for the synthetic put and the actual put. A synthetic short put can be created by selling a call of the same month and strike, and then buying stock on a share-for-share basis. This is indicated mathematically by
multiplying both sides of the put/call parity equation by –1: