JW Jones of Options Trading Signals explains how option traders can use the option greek delta to find profitable trades.
Options can be terribly confusing for the trader first encountering them. One of the most confusing concepts to understand is the interplay of the three primal forces of options—price of the underlying asset, time to expiration, and implied volatility.
The impact of each of these three factors on any given option position can be measured by its corresponding “Greek”. The “Greeks” corresponding to each of these factors are: delta-price, theta-time, and vega-implied volatility.
A fourth major Greek is gamma, and represents the change in delta as price of the underlying changes. Math majors among readers will recognize that gamma is the second derivative of delta.
The number of data points available to the options trader can be overwhelming, especially for the new trader first becoming familiar with these derivatives. It is important not to get lost in the data available and to focus on the decisions at hand.
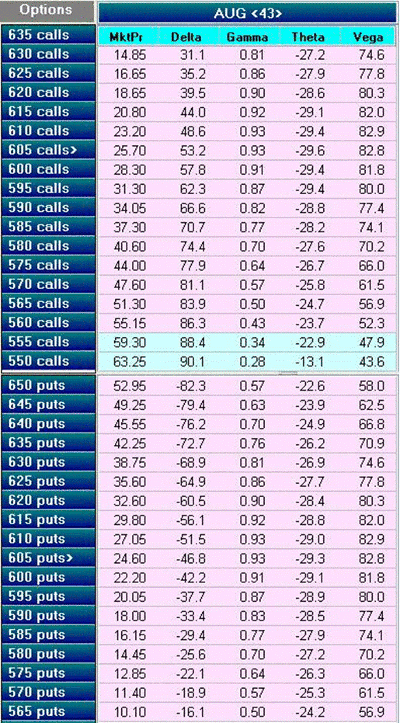
Consider the tremendous amount of information available on the following small portion of the options montage for Apple (AAPL). For this article I want to focus on delta and gamma exclusively.
Delta is a measure of the correlation of price change of an option relative to the price change of the underlying. It is a very dynamic attribute, and can potentially range from 0 to 1 for individual calls and 0 to -1 for individual puts. Delta is always a positive number for calls and a negative number for puts.
A call option with a delta of 0.5 would move up 50¢ for the first dollar increase in the price of the underlying. As an example, consider AAPL, which is trading at $605 per share. The August 605 call has a delta of 53.2 and would increase in value 53.2¢ as the price of AAPL traded up to $606. To provide a point of reference for the stock trader, each individual share of stock can be thought of to have a delta of one.
Remember that the delta of any individual option is not a constant value, but increases and decreases as price of the underlying changes. Gamma represents the rate of change of delta as the strike price of an option moves closer to or farther from the current market price of the underlying. The dynamic nature of delta is a critical point of understanding for the successful options trader.
Gamma values for both puts and calls are positive. As an example, our August 605 AAPL call has a gamma of 0.93. As price moves from 605 to 606, delta will increase from 53.2 to (53.2+0.93) = 54.13.
This dynamic nature of delta has the net result of a positive gamma position becoming increasingly long or short as price moves in the predicted direction. Conversely, the trader holding a negative gamma position becomes increasingly long or short inverse to the market’s direction.
In practical use, delta has some exceedingly helpful characteristics, and provides several useful benchmarks for the trader. One particularly interesting characteristic of delta is its relationship to our recent probability discussion.
The delta of any given option is a rough approximation of the probability that it will expire in-the-money. Therefore, our August AAPL 605 call with a delta of 53.2 has around a 53.2% probability of being in the money at expiration.
This correlation of the delta with the probability of expiring in the money has great utility in selecting trades. For example, knowing this probability relationship, the iron condor trader can easily select the strike with the probability of success appropriate for his risk tolerance.
Another helpful and consistent observation is that the at-the-money strike always has a delta of around 50 for calls and -50 for puts. In-the-money strikes always have deltas with an absolute value greater than 50 and out of the money strikes have deltas with absolute values less than 50.
An infrequently discussed characteristic of delta is its behavior in relation to time to expiration. Immediately before the moment of expiration, an individual option must have a delta of either 0 or 100, and as it approaches its point of expiration, the delta begins to rise or fall to meet that value.
In future articles, we will tackle the issues of the other Greeks.
At this point, suffice it to say that an intimate familiarity with the behavior of option positions predicted by the metrics reflected in the Greeks will give you a significant advantage in managing your option positions now and in the future.
JW Jones can be found at Options Trading Signals.